CpFit

CpFit program implements thermodynamic model of heat capacity and other thermodynamic functions based on usage of Einstein-Plank functions sum and empirical parameters. The used approach has been developed by Voronin et al. [1].

All thermodynamic functions (e.g. heat capacity, entropy and enthalpy) are represented as sums of Einstein-Plank terms:

C_p(T) = \sum_{i=1}^m \alpha_i C_\textrm{E}\left(\frac{\theta_i}{T}\right) ; \frac{C_\textrm{E}(x)}{R} = \frac{3x^2e^x}{\left(e^x - 1\right)^2}

S(T) - S(0) = \sum_{i=1}^m \alpha_i S_\textrm{E}\left(\frac{\theta_i}{T}\right) ; \frac{S_\textrm{E}(x)}{R} = 3\left[\frac{x}{e^{x} - 1} - \ln\left(1 - e^x\right)\right]

H(T) - H(0) = \sum_{i=1}^m \alpha_i \left[U_\textrm{E}\left(\frac{\theta_i}{T}\right) - U_0 \right] ; \frac{U_\textrm{E}(x) - U_0}{RT} = \frac{3x}{e^x - 1}

where \alpha_i and \theta_i are adjustable (usually by means of the least squares method) model parameters. They can be estimated from experimental data using least squares method. An exact universal gas constant value R=8.314462618~\mathrm{J\cdot mol^{-1} \cdot K^{-1}} from CODATA 2018 is used in the CpFit program. In the eqs \alpha_i values are dimensionless and \theta_i values are expressed in K. The software also supports usage of additional polynomial terms and separate support of heat capacity anomalies.

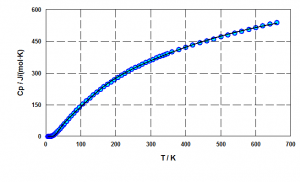
The thermodynamic model of heat capacity based on Einstein-Plank functions allows to approximate C_p(T), S(T)-S(0) and H(T)-H(0) in a wide temperature range using a unified set of parameters. Also unlike polynomial models it can give a physically correct extrapolation to a wider temperature range.

Implementation of this model in CpFit hides all analytical expressions and technical details and allow to use it as an ordinary statistical package for a nonlinear regression.

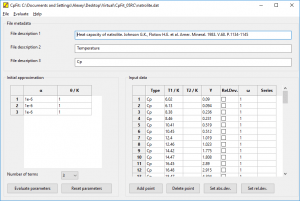
CpFit main window

CpFit main window

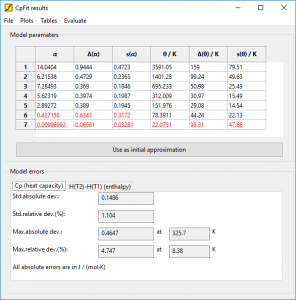
CpFit results window

CpFit results window

Approximation of heat capacity for natrolite

Approximation of heat capacity for natrolite

[1] Alexey L.Voskov, Ilya B.Kutsenok, Gennady F.Voronin CpFit program for approximation of heat capacities and enthalpies by Einstein-Planck functions sum // Calphad, 2018, 61, 50-61

[2] Gennady F. Voronin, Ilya B. Kutsenok Universal Method for Approximating the Standard Thermodynamic Functions of Solids // J. Chem. Eng. Data, 2013, 58, 2083−2094

[su_service title=”Download” icon=”icon: save” icon_color=”#777777″]

[su_spoiler title=”Installation and System Requirements” icon=”caret”]

CpFit program has the next system requirements:

  • Microsoft Windows XP/Vista/7/8/8.1/10 (32-bit or 64-bit)
  • 256 Mb of RAM
  • 5 Mb of free disk space
  • SVGA with 1024×768 resolution or higher

The program doesn’t require any installation. You can just unpack an archive with the program and begin the work.

If you want to make the program from the source code (that is not required) you will need:

  • GCC C++ compiler 4.5.2 or higher and MinGW environment
  • wxWidgets 3.0.2 or higher
  • levmar 2.6 or higher
  • lua 5.3 or higher (as static or dynamic library)
  • Doxygen is not required but highly recommended (to generate documentation about the
    source code)

More detailed information about compilation and linking is given in the source code.
[/su_spoiler]

[/su_service]