Программа CpFit

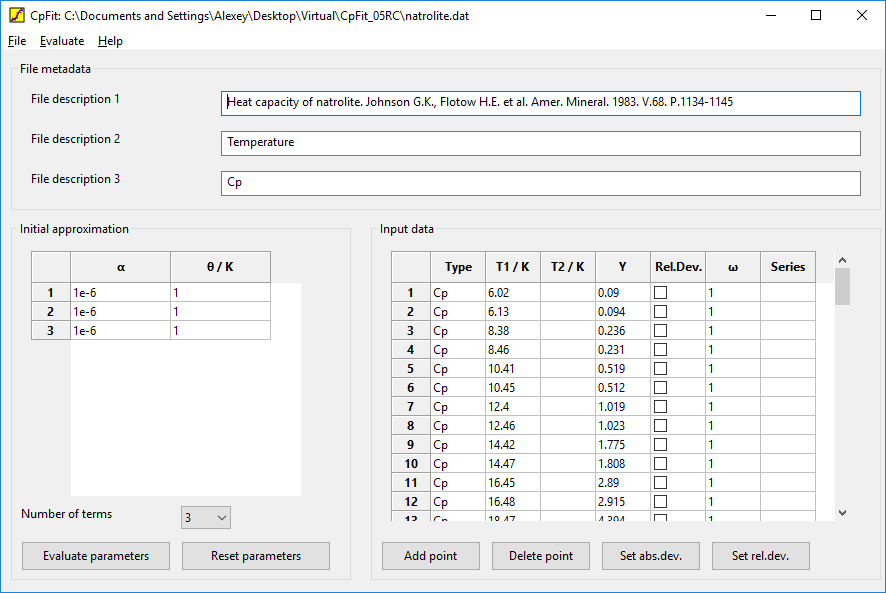
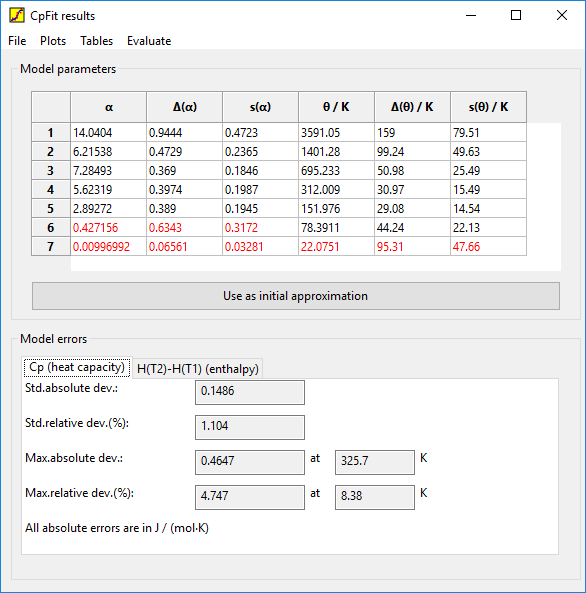
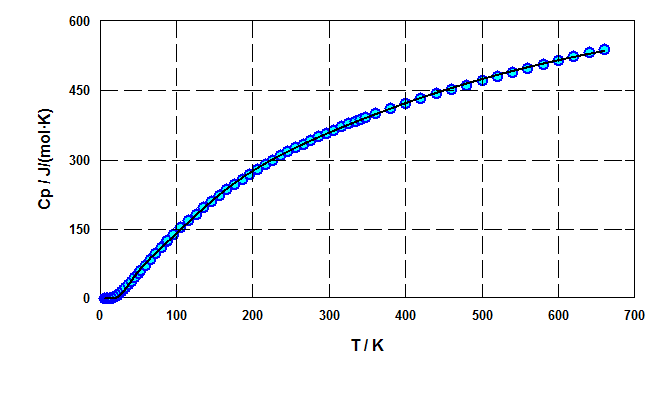
В программе CpFit реализована термодинамическая модель теплоёмкости и других термодинамических функций, основанная на использовании суммы функций Эйнштейна-Планка и эмпирических параметров. Использованный подход был разработан Г.Ф. Ворониным и др.[1].

Все термодинамические функции (теплоёмкость, энтропия, энтальпия) представлются в виде суммы вкладов в виде функций Эйнштейна-Планка:

C_p(T) = \sum_{i=1}^m \alpha_i C_\textrm{E}\left(\frac{\theta_i}{T}\right) ; \frac{C_\textrm{E}(x)}{R} = \frac{3x^2e^x}{\left(e^x - 1\right)^2}

S(T) - S(0) = \sum_{i=1}^m \alpha_i S_\textrm{E}\left(\frac{\theta_i}{T}\right) ; \frac{S_\textrm{E}(x)}{R} = 3\left[\frac{x}{e^{x} - 1} - \ln\left(1 - e^x\right)\right]

H(T) - H(0) = \sum_{i=1}^m \alpha_i \left[U_\textrm{E}\left(\frac{\theta_i}{T}\right) - U_0 \right] ; \frac{U_\textrm{E}(x) - U_0}{RT} = \frac{3x}{e^x - 1}

где \alpha_i и \theta_i – это оптимизируемые (обычно с помощью метода наименьших квадратов) параметры модели. Они могут быть оценены из экспериментальных данных методом наименьших квадратов. В программе CpFit используется точное значение универсальной газовая R=8.314462618~\mathrm{J\cdot mol^{-1}\cdot K^{-1}} из CODATA 2018. В приведенных выше уравнениях значения \alpha_i безразмерны, а значения \theta_i выражаются в K. Программа также поддерживает добавление полиномиальных слагаемых в модель теплоёмкости и позволяет отдельно обрабатывать аномалии теплоёмкости.

Термодинамическая модель теплоёмкости, основанная на функциях Эйнштейна-Планка, позволяет аппроксимировать C_p(T), S(T)-S(0) и H(T)-H(0) в широком температурном диапазоне, используя один набор параметров. Также в отличие от полиномиальных моделей она может обеспечить физически корректную экстраполяцию на более широкий температурный интервал.

Реализация этой модели в программе CpFit скрывает от пользователя все аналитические выражения и технические детали, что позволяет использовать её как обычный статистический пакет для нелинейной регрессии.

CpFit main window
Главное окно программы CpFit
CpFit results window
Окно программы CpFit с результатами
Описание теплоёмкости натролита

[1] Alexey L. Voskov, Ilya B. Kutsenok, Gennady F. Voronin CpFit program for approximation of heat capacities and enthalpies by Einstein-Planck functions sum // Calphad, 2018, 61, 50-61

[2] Gennady F. Voronin, Ilya B. Kutsenok Universal Method for Approximating the Standard Thermodynamic Functions of Solids // J. Chem. Eng. Data, 2013, 58, 2083−2094

Скачать

Дистрибутив программы + руководство пользователя (версия от 07 ноября 2020 г.)
Исходные тексты программы (распространяются по лицензии GNU GPL версии 2.0 или выше)

Минимальные системные требования для программы CpFit:

  • Microsoft Windows XP/Vista/7/8/8.1/10 (32-bit или 64-bit)
  • 256 Мб ОЗУ
  • 5 Мб места на диске
  • SVGA с разрешением 1024×768 или выше

Программа не требует какой-либо установки. Вы можете просто распаковать архив с программой и начинать работу.

Если Вы желаете собрать программу из исходного кода (что не требуется для работы), то Вам понадобятся:

  • Компилятор GCC C++ версии 4.5.2 или выше и среда MinGW
  • Библиотека wxWidgets версии 3.0.2 или выше
  • Библиотека levmar версии 2.6 или выше
  • Библиотека lua версии 5.3
  • Doxygen не требуется, но крайне рекомендуется (для генерации документации по исходному коду)

Более подробная информация о компиляции и компоновке дана в исходном коде.

Задача для практикума

Программа CpAppro
Описание
Первичные данные
Шаблон оформления